Lineare Zusammenhänge II

Datensatz

Wir benutzen wieder den Datensatz df_wide aus der letzten Woche. Hier nochmal eine Übersicht:

Variable	Inhalt
group	Treatment-Gruppe
pre_skill	motorischer Skill vor dem Treatment
post_skill	motorischer Skill nach dem Treatment
hawie_iq	Intelligenz-Quotient aus HAWIE
hawie_wahr_log	Skalenwert wahrnehmungsgebundenes logisches Denken aus HAWIE

Multiple Lineare Regression

Verfahren

Bei der multiplen linearen Regression dienen mehrere quantitative oder dichotome Variablen \(X_j\) als Prädiktoren zur Vorhersage des quantitativen Kriteriums \(Y\). Die Vorhersagegleichung hat hier die Form \(\hat{Y} = a + b_1 X_1 + ... + b_j X_ j + ... + b_p X_p\) , wobei die Koeffizienten \(a\) und \(b_j\) auf Basis der empirischen Daten zu ermitteln sind.

Als R-formula sieht das wie folgt aus:

\[\text{Kriterium} \sim \text{Prädiktor}_1 + \dots + \text{Prädiktor}_p\]

Man versucht also, eine stetige Variable durch eine Linearkombination mehrerer Variablen vorherzusagen. Dabei ist aber meistens eher das Ausmaß des Zusammenhangs als die tatsächliche Vorhersage für neue Werte interessant.

Deskriptive Modellanpassung und Regressionsanalyse

Regression vom motorischen Skill nach dem Training auf IQ und wahrnehmungsgebundenes logisches Denken:

fit_post_il <- df_wide %>% 
   lm(post_skill~hawie_iq+hawie_wahr_log, 
      data=.)

fit_post_il

## 
## Call:
## lm(formula = post_skill ~ hawie_iq + hawie_wahr_log, data = .)
## 
## Coefficients:
##    (Intercept)        hawie_iq  hawie_wahr_log  
##        5.75745        -0.05013         0.42397

Für standardisierte Gewichte wie vorher:

library(magrittr)
fit_post_il_z <- df_wide %>% 
  mutate(across(where(is.numeric), ~scale(.))) %$% 
   lm(post_skill~hawie_iq+hawie_wahr_log)

Darstellung

Mit der Funktion scatter3d() aus dem Paket car lassen sich die Daten dann dreidimensional mit Residuen plotten.

library(car)

scatter3d(post_skill~hawie_iq+hawie_wahr_log, 
          data=df_wide)

Ein bisschen komplizierter geht das auch mit dem Paket plotly. Dafür muss zuerst ein Datensatz erstellt werden, der den gesamten Raum der im darzustellenden Datensatz vorliegenden Prädiktoren abdeckt:

dummy <-  df_wide %>% 
  select(hawie_iq, hawie_wahr_log) %>% 
  expand.grid()

Für alle diese Kombinationen müssen wir jetzt mit unserem Modell eine Vorhersage treffen:

dummy$post_skill <- predict(fit_post_il, dummy)

Und diesen Datensatz können wir jetzt mit plotly darstellen:

library(plotly)

plot_ly(data = df_wide,
        x = ~hawie_iq,
        y = ~hawie_wahr_log,
        z = ~post_skill,
        type = 'scatter3d',
        mode = 'markers') %>% 
  add_mesh(data = dummy)

Regressionsdiagnostik

Regressionsdiagnostik

Regressionsgleichungen sind sehr anfällig für verschiedene Klassen von Ausreißern. Ein Extremwert kann unter bestimmten Bedingungen die errechneten Koeffizienten extrem beeinflussen und verzerren.

Es gibt drei Klassen von diagnostischen Werten, die unterschiedliche Aspekte möglicher Verfälschung beleuchten.

1. Abstand (mögliche Ausreißer im Wertebereich des Kriteriums)

2. Hebelwirkung (mögliche Ausreißer im Wertebereich der Prädiktoren)

3. Einfluss (Kombination von Abstand und Hebelwirkung)

http://omaymas.github.io/InfluenceAnalysis/ gibt es eine Shiny-App, mit der man daran rumspielen kann.

Abstand

Die Plausibilität des Abstandes lässt sich am Besten mit Hilfe der Residuen der Regression überprüfen. Dafür benutzen wir hier eine grafische Darstellung, um einen Überblick über deren Verteilung zu erlangen.

df_wide %>% 
  mutate(Residuen = residuals(fit_post_il)) %>% 
ggplot(aes(y = Residuen, x = '') ) +
  geom_violin(color = 'grey', fill = 'lightgrey',
              alpha = .5) +
  geom_boxplot(width = .5) +
  coord_flip()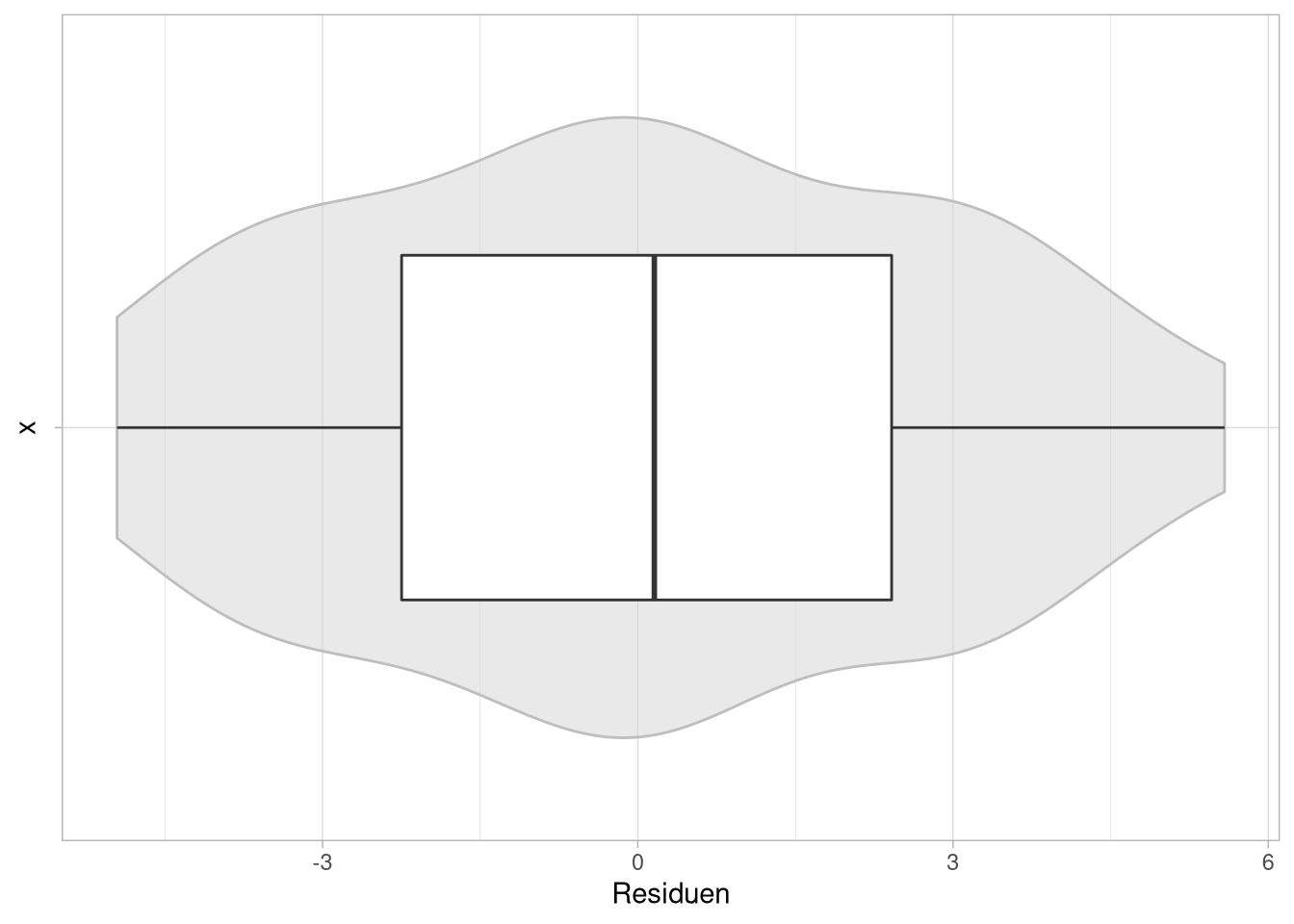

Hebelwirkung

Hebelwirkung ist das Ausmaß, in dem ein Prädiktor-Wert ungewöhnlich in Bezug auf die restlichen Prädiktorwerte ist. Das für Aussagen darüber genutzte Maß sind die Hebelwerte. Bei der einfachen Regression sind Hebelwerte die Abweichung der einzelnen Prädiktorwerte von deren Mittelwert. Bei der multiplen Regression ist das nicht ganz so einfach.

In beiden Fällen bewegt sich der Hebelwert aber zwischen \(\frac{1}{N}\) und 1.

Diese Hebelwerte werden mit hatvalues() berechnet.

Faustregel: Bei \(p\) Einflussgrößen (Prädiktoren) und \(N\) Beobachtungen sind Fälle mit Hebelwerten von größer als \(3 \cdot \frac{p+1}N\) problematisch.

h <- hatvalues(fit_post_il)

Mit einem Spikeplot lassen sich diese dann veranschaulichen.

tibble(hats = h,
       ID = 1:50) %>% 
  ggplot(aes(x= ID, ymax = h, ymin= 0)) +
  geom_linerange() +
  geom_hline(yintercept = (3*(2+1)/50),col='red') +
  scale_x_continuous(breaks = seq(0,50,5)) +
  labs(y = 'hat-values')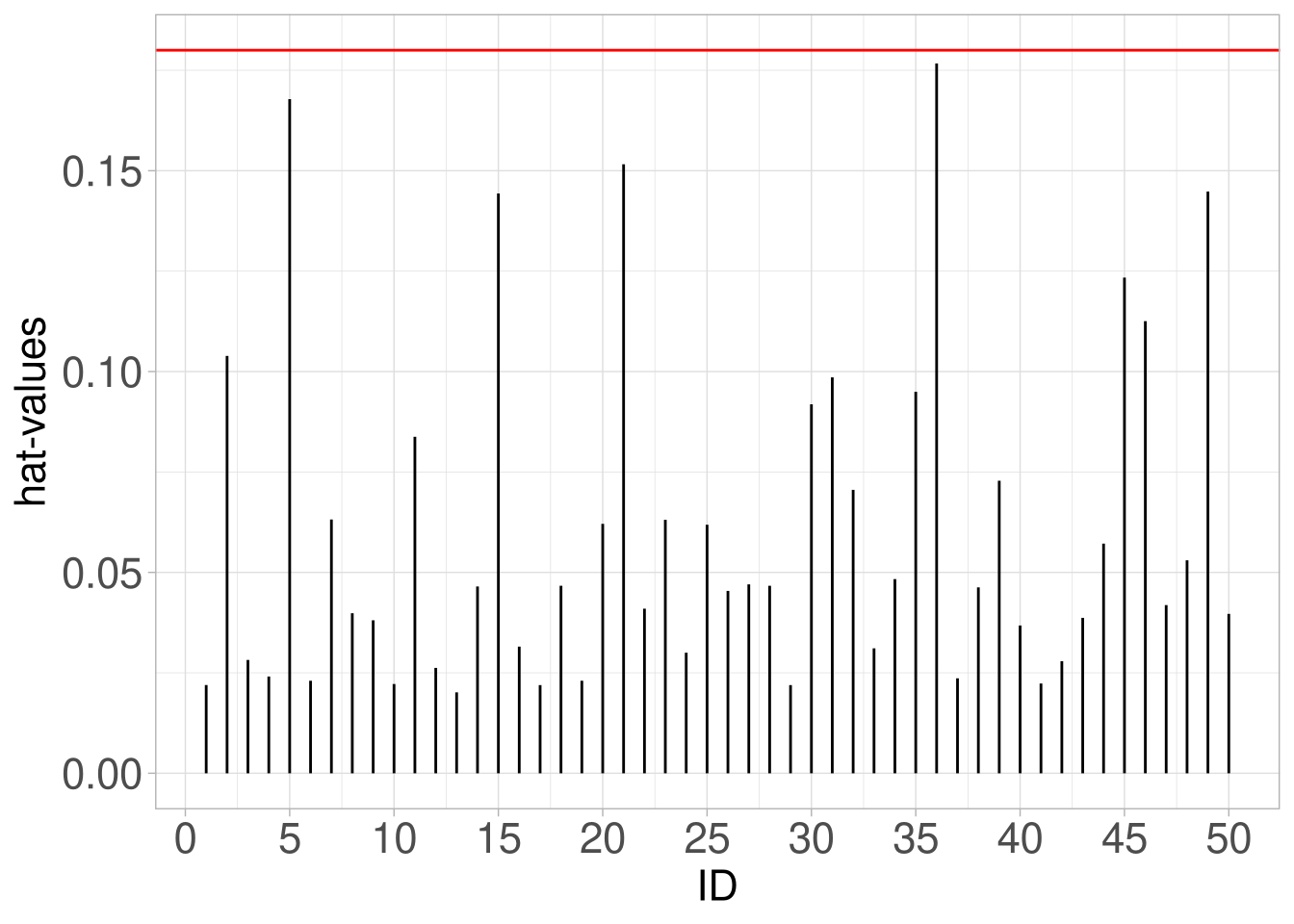

Einfluss

Unter Einfluss oder influence versteht man den Einfluss eines einzelnen Datenpunktes auf die gesamte Vorhersage. Er stellt also eine Kombination der vorher genannten Parameter dar.

Am besten lässt sich dieser mit folgender Funktion grafisch überprüfen:

plot(fit_post_il, which = 5)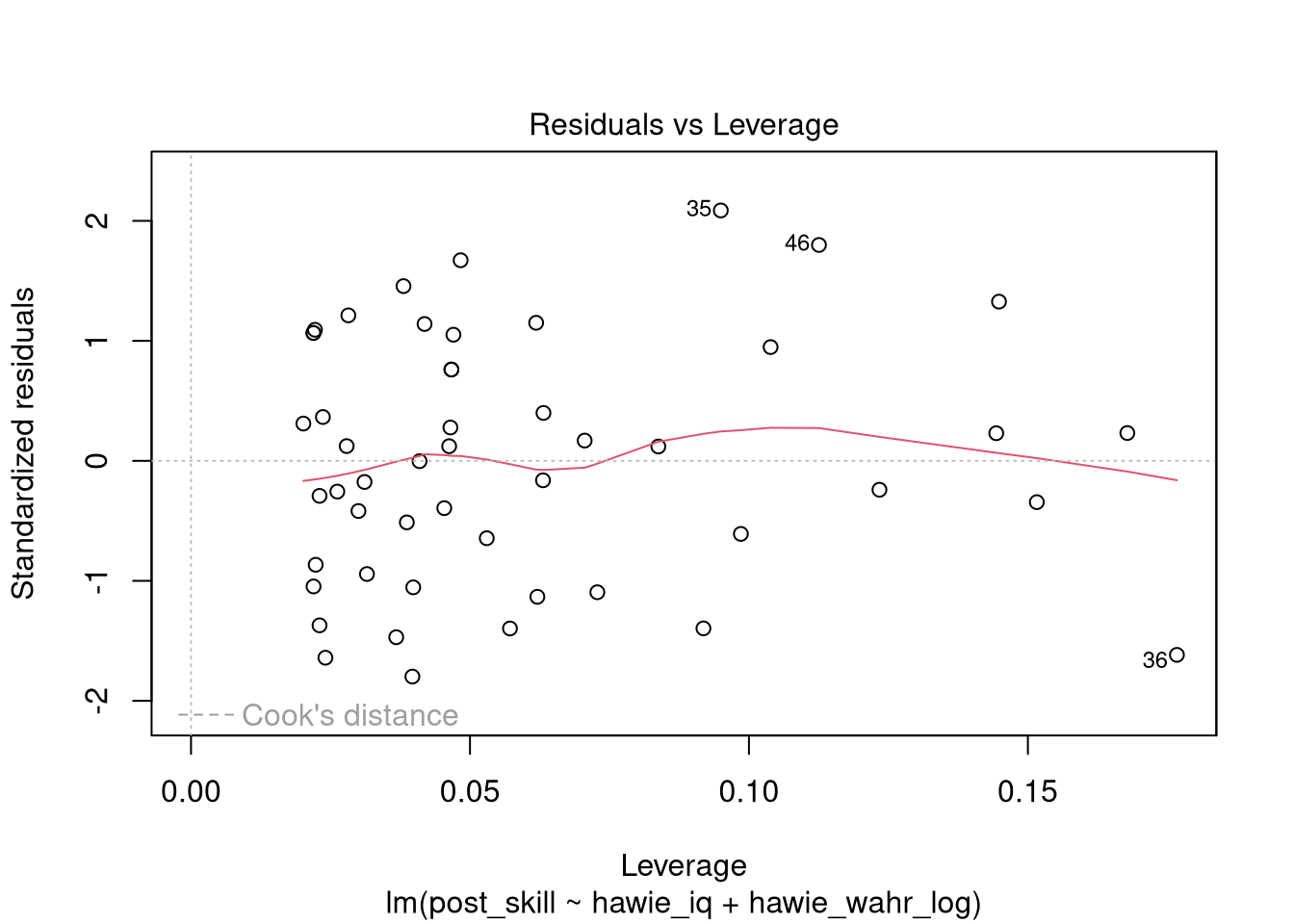

Ganz hübsche Alternativen bieten auch die Funktion influencePlot() aus dem car-Paket:

influencePlot(fit_post_il)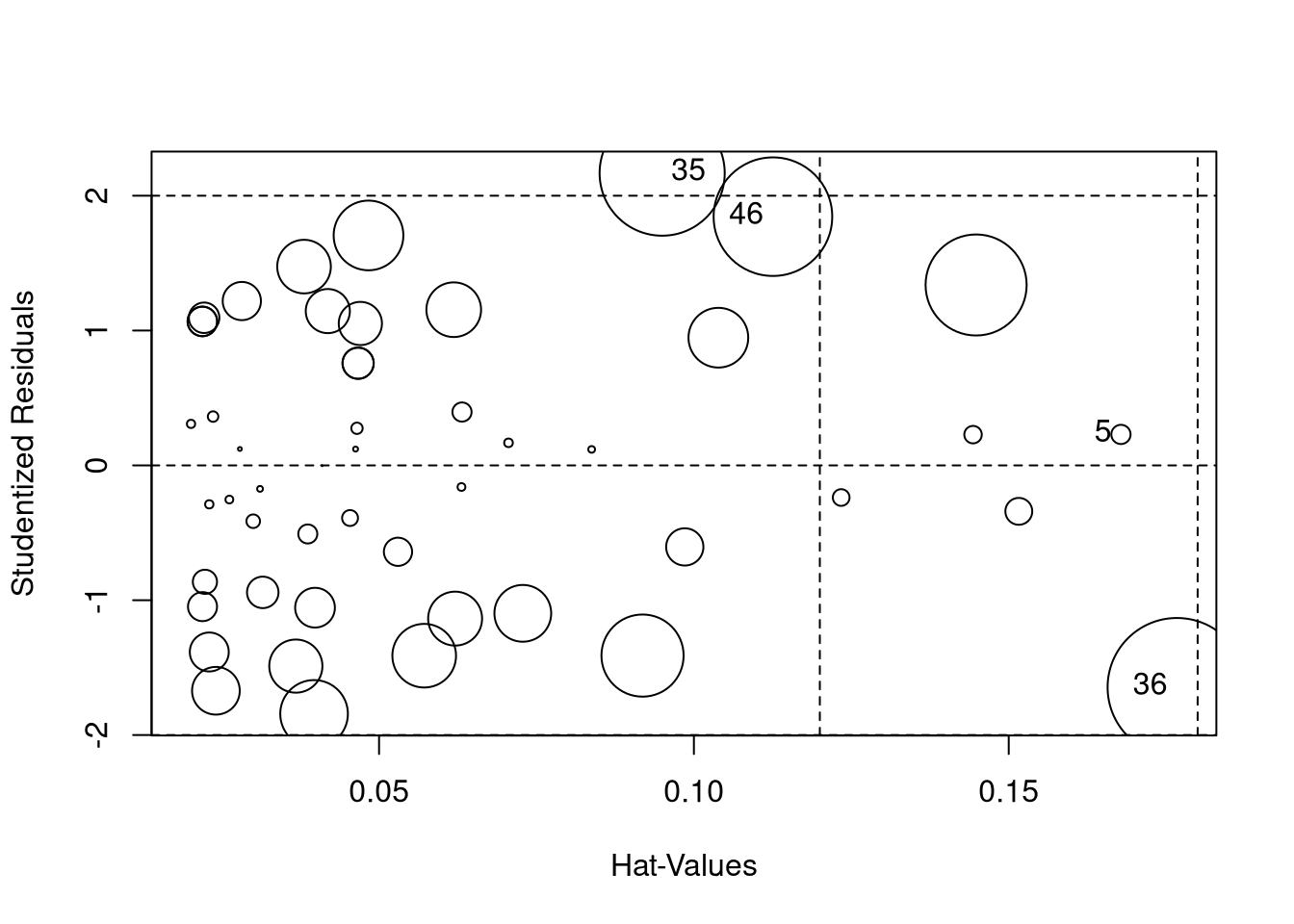

Tab. 3:

StudRes	Hat	CookD
0.229	0.168	0.00361
2.17	0.095	0.152
-1.65	0.177	0.187
1.84	0.113	0.137

Außerdem können wir uns auch hier das broom-Paket benutzen, diesmal um uns alle diagnostischen Werte in einem praktischen Datensatz ausgeben zu lassen:

fit_post_il %>% 
  broom::augment()

Tab. 4:

post_skill	hawie_iq	hawie_wahr_log	.fitted	.resid	.hat	.sigma	.cooksd	.std.resid
2	93	9	4.91	-2.91	0.022	2.81	0.0082	-1.05
9	121	16	6.48	2.52	0.104	2.82	0.0347	0.948
8	90	8	4.64	3.36	0.0282	2.8	0.0142	1.21
1	97	11	5.56	-4.56	0.0241	2.76	0.0221	-1.64
8	94	15	7.41	0.595	0.168	2.84	0.00361	0.232
4	95	9	4.81	-0.811	0.023	2.84	0.000669	-0.292
5	96	7	3.91	1.09	0.0632	2.84	0.00358	0.399
3	107	13	5.91	-2.91	0.0398	2.81	0.0154	-1.05
10	97	12	5.98	4.02	0.0381	2.78	0.028	1.46
8	92	9	4.96	3.04	0.0222	2.81	0.00904	1.09
6	120	14	5.68	0.322	0.0838	2.84	0.000436	0.12
4	97	9	4.71	-0.711	0.0262	2.84	0.000589	-0.256
6	97	10	5.13	0.865	0.0201	2.84	0.000661	0.311
5	98	8	4.24	0.763	0.0465	2.84	0.00125	0.278
8	111	17	7.4	0.599	0.144	2.84	0.00298	0.23
2	99	9	4.61	-2.61	0.0315	2.82	0.00965	-0.943
8	99	10	5.03	2.97	0.0219	2.81	0.0085	1.07
8	90	11	5.91	2.09	0.0467	2.83	0.00945	0.761
1	95	9	4.81	-3.81	0.023	2.79	0.0148	-1.37
1	101	8	4.09	-3.09	0.0621	2.8	0.0283	-1.13
2	91	4	2.89	-0.892	0.152	2.84	0.00706	-0.344
5	108	11	5.01	-0.00743	0.041	2.84	1.03e-07	-0.0027
4	77	6	4.44	-0.442	0.0631	2.84	0.00059	-0.162
4	105	11	5.16	-1.16	0.03	2.84	0.0018	-0.418
8	77	7	4.87	3.13	0.0619	2.8	0.0291	1.15
5	95	12	6.08	-1.08	0.0454	2.84	0.00246	-0.394
7	92	7	4.11	2.89	0.047	2.81	0.0182	1.05
8	90	11	5.91	2.09	0.0467	2.83	0.00945	0.761
8	99	10	5.03	2.97	0.0219	2.81	0.0085	1.07
1	71	6	4.74	-3.74	0.0918	2.78	0.0657	-1.4
5	118	16	6.63	-1.63	0.0986	2.83	0.0135	-0.609
5	75	6	4.54	0.458	0.0706	2.84	0.000723	0.169
4	93	8	4.49	-0.487	0.0311	2.84	0.000331	-0.176
10	83	9	5.41	4.59	0.0483	2.76	0.0473	1.67
9	89	5	3.42	5.58	0.095	2.71	0.152	2.09
1	131	14	5.13	-4.13	0.177	2.76	0.187	-1.62
6	100	10	4.98	1.02	0.0236	2.84	0.00108	0.365
5	81	7	4.66	0.335	0.0463	2.84	0.000241	0.122
2	75	7	4.97	-2.97	0.0728	2.81	0.0314	-1.09
1	107	11	5.06	-4.06	0.0368	2.78	0.0275	-1.47
3	100	11	5.41	-2.41	0.0223	2.82	0.00571	-0.866
6	95	11	5.66	0.341	0.0279	2.84	0.000145	0.123
3	86	7	4.41	-1.41	0.0387	2.84	0.00353	-0.513
1	78	7	4.82	-3.82	0.0572	2.78	0.0394	-1.4
6	84	12	6.63	-0.634	0.123	2.84	0.00272	-0.241
9	115	10	4.23	4.77	0.113	2.74	0.137	1.8
9	91	11	5.86	3.14	0.0419	2.8	0.0189	1.14
3	79	7	4.77	-1.77	0.053	2.83	0.00776	-0.645
10	128	17	6.55	3.45	0.145	2.79	0.0994	1.33
1	106	13	5.96	-4.96	0.0397	2.74	0.0445	-1.8

Test der Regressionskoeffizienten

Auch bei der multiplen linearen Regression lassen sich die Regressionskoeffizienten der einzelnen Prädiktoren jeweils auf die Nullhypothese testen, dass die jeweiligen “wahren Koeffizienten” \({b_i}^*\) gleich 0 sind. Die Schätzung der Streuung der Koeffizienten ist ein bisschen komplizierter als im einfachen Fall, deswegen sei hier nur erwähnt, dass es geht.

Die für jeden Prädiktoren gebildete Teststatistik \(t = \frac{b_i}{s_{b_{i}}}\) ist dann bei Gültigkeit der Nullhypothese (\(H_0:{b_i}^* = 0\)) \(t_{N-p-1}\)-verteilt, wobei \(p\) die Gesamtzahl der Prädiktoren und \(N\) die Gesamtzahl der Beobachtungen ist.

Der Test der Parameter auf Signifikanz läuft wie im einfachen Fall mit der Funktion summary()

summary(fit_post_il_z)

## 
## Call:
## lm(formula = post_skill ~ hawie_iq + hawie_wahr_log)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.70753 -0.77446  0.05423  0.83241  1.92405 
## 
## Coefficients:
##                  Estimate Std. Error t value Pr(>|t|)
## (Intercept)     6.812e-17  1.371e-01   0.000   1.0000
## hawie_iq       -2.331e-01  2.127e-01  -1.096   0.2787
## hawie_wahr_log  4.524e-01  2.127e-01   2.127   0.0387
##                 
## (Intercept)     
## hawie_iq        
## hawie_wahr_log *
## ---
## Signif. codes:  
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.9692 on 47 degrees of freedom
## Multiple R-squared:  0.09891,    Adjusted R-squared:  0.06057 
## F-statistic:  2.58 on 2 and 47 DF,  p-value: 0.0865

Oder auch wieder mit broom::tidy():

broom::tidy(fit_post_il_z)

Tab. 5:

term	estimate	std.error	statistic	p.value
(Intercept)	6.81e-17	0.137	4.97e-16	1
hawie_iq	-0.233	0.213	-1.1	0.279
hawie_wahr_log	0.452	0.213	2.13	0.0387

Aufgabe

Tab. 6:

term	estimate	std.error	statistic	p.value
(Intercept)	6.81e-17	0.137	4.97e-16	1
hawie_iq	-0.233	0.213	-1.1	0.279
hawie_wahr_log	0.452	0.213	2.13	0.0387

Wie lässt sich das Ergebnis interpretieren?

1. Der IQ liefert einen signifikanten Beitrag zur Vorhersage des motorischen Skills nach dem Training.
2. Es gibt keine Korrelation zwischen IQ-Werten und dem motorischen Skill nach dem Training.
3. Größere Werte auf der Skala für wahrnehmungsgebundenes logisches Denken bewirken eine signifikante Steigerung des motorischen Skills nach dem Training.
4. Die Werte der Vorhersage steigen mit denen des wahrnehmungsgebundenen logischen Denkens und die Werte für wahrnehmungsgebundenes logisches Denken leisten einen signifikanten Beitrag zur Vorhersage des motorischen Skills nach der Intervention.

Antwort

Viertens kann man so sagen.

Gegen 3 spricht die Kausalinterpretation, 1 ist verkehrt (keine Signifikanz) und über 2 können wir mit dem Ergebnis des Gesamtmodells direkt keine Aussage treffen.

Test der Signifikanz von \(\text{R}^2\)

Man kann sich die Frage stellen, ob das Modell mit den gewählten Prädiktoren insgesamt das Kriterium gut vorhersagt. Das lässt sich am einfachsten bewerkstelligen, indem man den Determinationskoeffizienten \(R^2\) auf die \(\text{H}_0\) testet, dass der ‘wahre’ Koeffizient \(R^*\) der Population gleich 0 ist. (“\(\text{H}_0: R^* = 0\)”)

Getestet wird diese Hypothese mit der Teststatistik \(F = \frac{(N-p-1)R^2}{p(1-R^2)}\), die \(F_{p,N-p-1}\)-verteilt ist. Dabei ist \(N\) wieder die Anzahl der Beobachtungen und \(p\) die Anzahl der Prädiktoren.

Um diesen Test durchzuführen können wir entweder auf den unteren Teil des summary-Outputs für ein Regressionsmodell gucken:

## Residual standard error: 0.9692 on 47 degrees of freedom
## Multiple R squared: 0.0989 , Adjusted R-squared: 0.0606
## F-statistic:  2.58 on 2 and 47 DF, p-value: 0.0865

Oder die broom::glance()-Funktion nutzen:

fit_post_il_z %>% 
  broom::glance()

Tab. 7:

r.squared	adj.r.squared	sigma	statistic	p.value	df	logLik	AIC	BIC	deviance	df.residual	nobs
0.0989	0.0606	0.969	2.58	0.0865	2	-67.8	144	151	44.2	47	50

Aufgabe

Tab. 8:

r.squared	adj.r.squared	sigma	statistic	p.value	df	logLik	AIC	BIC	deviance	df.residual	nobs
0.0989	0.0606	0.969	2.58	0.0865	2	-67.8	144	151	44.2	47	50

Wie lässt sich das Ergebnis interpretieren?

1. Unser Modell ist ein sehr gutes Modell, es klärt einen signifikanten Teil der Varianz auf.

2. Unser Modell sagt den motorischen Skill nicht gut voraus.

3. Unser Modell klärt \(\sim\) 10% der Varianz auf.

Antwort

2 und 3 lassen sich so sagen.

Prüfung der Voraussetzungen

Für die Tests auf Signifikanz in der konventionellen Regressionsanalyse gelten die Voraussetzungen der Varianzhomogenität und der Normalverteiltheit der Residuen für jede einzelne Prädiktor-Kombination. Wir setzen also wieder voraus, dass \(Y\) für jede Kombination der \(X_p\) normalverteilt ist mit \(\mu = b_1^*X_1 + \dots + b_p^*X_p + a^*\) und einer Varianz \(\sigma^2\).

Zusätzlich zu den Voraussetzungen ist für die multiple Regression das Ausmaß der Multikollinearität der Prädiktoren relevant.

Grafische Prüfverfahren

Um die Anforderungen an die Messfehler der Regression heuristisch zu überprüfen, lassen sich verschiedene grafische Darstellungen heranziehen. Dazu benutzt man am besten eine standardisierte Form der Residuen. Zwei davon haben sich durchgesetzt, zum einen die

studentischen \[E_{stud}=\frac{\frac{E}{s}}{(1-\frac{1}{N} + h)^{\frac{1}{2}}}\] und zum anderen die standardisierten \[E_{stan}=\frac{Y - \hat{Y}}{\sqrt{\frac{1}{n}\sum_{i=1}^n e_i^2}}\] Residuen. Die Residuen lassen sich dafür mit rstudent() oder rstandard() berechnen.

Hier wird die broom::augment()-Funktion praktisch, da wir in dem ausgegebenen Datensatz die Residuen und die vorhergesagten Werte praktisch aufbereitet haben

Die Verteilungseigenschaften können wir dann grafisch-heuristisch mit einem qq-Plot überprüfen:

fit_post_il %>% 
  broom::augment() %>% 
  ggplot(aes(sample = .std.resid)) +
  geom_qq() +
  geom_qq_line()

Je weiter die Punkte von der eingezeichneten Gerade abweichen, desto weniger können wir von einer Normalverteiltheit der Residuen ausgehen. Wie groß “noch akzeptable” Abweichung ist, ist ein Stück weit Gefühlssache.

Hier findet man eine kleine shiny-App, mit der an qq-plots rumgespielt werden kann:

Die Voraussetzung der Varianzhomogenität lässt sich auch so verstehen, dass wir für Y für jede Werte-Kombination unserer Prädiktoren eine gleich große Varianz voraussetzen. Über den Verlauf unserer vorhergesagten Werte sollten wir also um den 0-Punkt ungefähr gleich (breit) streuende Residuen beobachten können. Die genaue Form ist dabei aber natürlich abhängig von der Verteilung der Prädiktoren. Wenn wir diesem Plot jetzt noch einen lokalen Schätzer des Mittelwerts hinzufügen, haben wir einen so genannten Spread-Level-Plot:

fit_post_il %>% 
  broom::augment() %>%
  ggplot(aes(x = .fitted, y = .std.resid)) +
  geom_point() +
  geom_hline(yintercept = 0, color = 'red') +
  geom_smooth(formula = 'y~x',se = F, method = 'loess')

In unserem Fall haben wir scheinbar ein paar Ausreißer (wie vorher auch schon gesehen), sonst ist die Punktwolke aber unproblematisch. Die Abweichung der loess-Regression sieht oft dramatischer aus als es faktisch ist, vor allem bei wenigen Beobachtungen wie bei uns.

Man muss immer im Hinterkopf behalten, dass das genaue Bild stark von der Verteilung der Prädiktoren abhängt. So ist keins der folgenden Muster wirklich eine typische Punktwolke, trotzdem sind die Voraussetzungen überall gegeben:

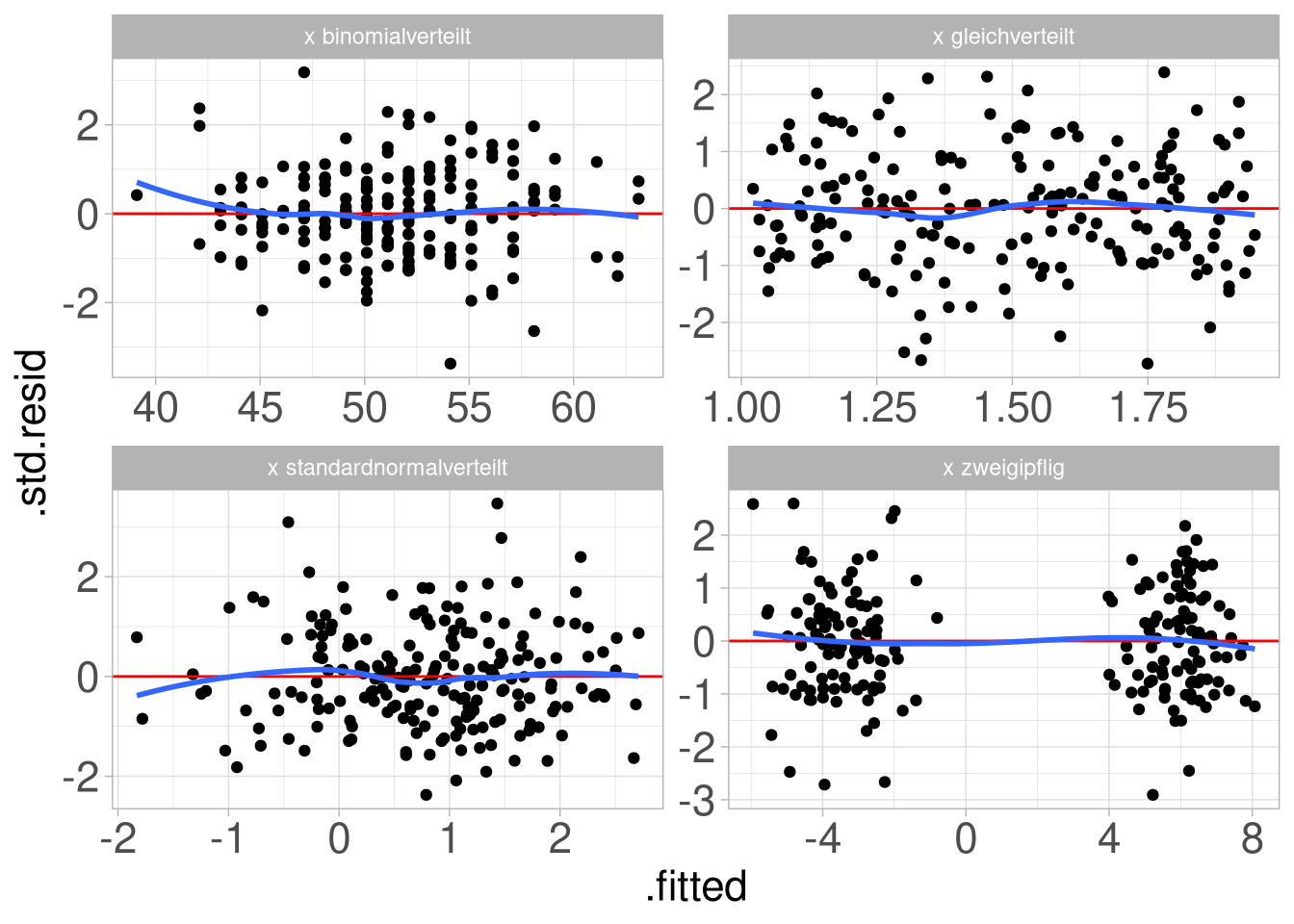
Wirklich Grund zur Sorge sollten uns Bilder wie die folgenden geben:

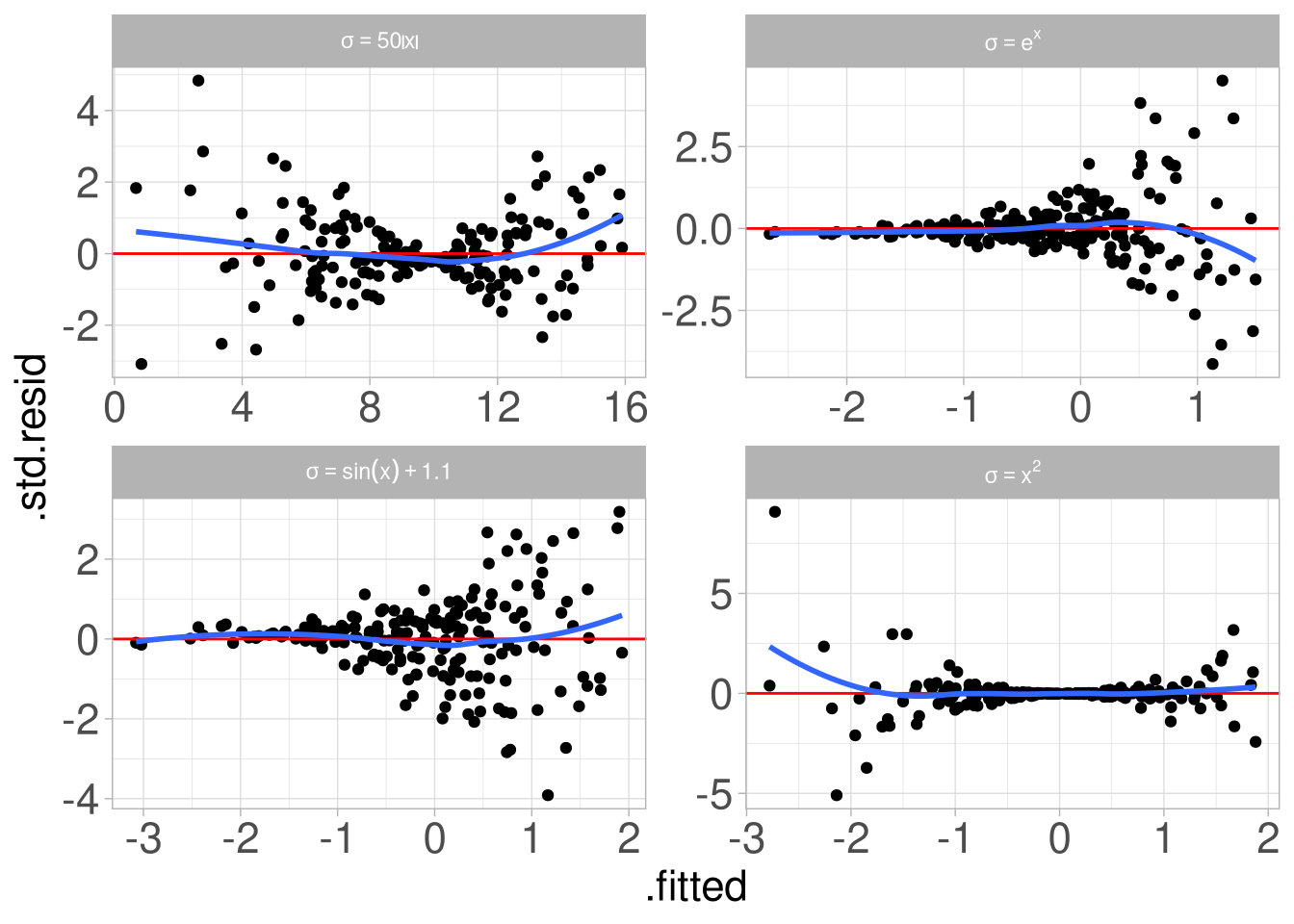
Inferenzstatistischer Test der Voraussetzungen

Inferenz-statistisch lässt sich die Normalverteilung der Residuen zum Beispiel mit dem Kolmogorov-Smirnov-Test überprüfen:

ks.test(x = rstudent(fit_post_il),
        y = 'pnorm')

## 
##  Asymptotic one-sample Kolmogorov-Smirnov test
## 
## data:  rstudent(fit_post_il)
## D = 0.093678, p-value = 0.7726
## alternative hypothesis: two-sided

Aufgabe

## 
##  Asymptotic one-sample Kolmogorov-Smirnov test
## 
## data:  rstudent(fit_post_il)
## D = 0.093678, p-value = 0.7726
## alternative hypothesis: two-sided

Wie lässt sich das Ergebnis interpretieren? 1. \(1-p\) ist kleiner als 30%, deswegen können wir keine Normalverteilung annehmen. 2. p ist größer als 20%; da wir eine Normalverteiltheit nicht ausschließen können, nehmen wir diese Voraussetzung als gegeben an. 3. Wir können gar nichts sagen, der Test aller Residuen auf einmal ergibt keinen Sinn.

Antwort

Zweitens ist die übliche Interpretation, auch wenn dem Herrn Andres hier der Dampf aus den Ohren steigt.

Multikollinearität

Multikollinearität liegt dann vor, wenn sich die Werte eines Prädiktors gut aus einer Linearkombination der übrigen Prädiktoren vorhersagen lassen.

Dies ist insbesondere dann der Fall, wenn Prädiktoren paarweise miteinander hoch korrelieren.

Für die multiple Regression hat dies weniger stabile Schätzungen der Koeffizienten als unerwünschte Konsequenz. Das heißt für die Praxis, dass die Regressionsgewichte schwer interpretierbar werden, sobald die entsprechenden Prädiktoren zu stark korrelieren, da von Stichprobe zu Stichprobe starke Änderungen zu erwarten sind. Modelle mit Multikolliniaren Prädiktoren haben aber meistens relativ stabile Determinationskoeffizienten, wenn uns also so oder so nur das Gesamtmodell interessiert, ist Multikollinearität kein allzu großes Problem.

Als kleines Beispiel sind hier Simulationsergebnisse von 10000 Regressionen mit jeweils korrelierten Prädiktoren:

Die Regression wurden jeweils auf einem nach dem folgenden Schema simulierten Datensatz erstellt:

tibble(y = rnorm(100),
       x1 = y / 2 * runif(100,.5, 1.5),
       x2 = x1 * runif(100,.5, 1.5)) 

Tab. 9:

y	x1	x2
0.193	0.143	0.0999
1.02	0.735	0.816
0.813	0.21	0.186
0.954	0.361	0.218
2.08	0.931	1.01
1.61	0.71	1.02
0.19	0.142	0.152
-0.999	-0.336	-0.251
-0.615	-0.203	-0.142
3.32	1.41	1.54
0.922	0.545	0.431
1.23	0.467	0.32
-0.216	-0.142	-0.115
-1.34	-0.401	-0.443
-0.304	-0.153	-0.163
-0.0779	-0.0267	-0.0381
-0.193	-0.0836	-0.0737
0.123	0.0864	0.0447
-0.279	-0.16	-0.122
0.758	0.306	0.297
0.0606	0.0302	0.0388
-0.165	-0.0743	-0.0917
0.0715	0.0189	0.0136
0.649	0.22	0.261
1.1	0.359	0.369
-1.37	-0.553	-0.538
-0.127	-0.0864	-0.0849
1.08	0.804	1.09
-1.45	-0.736	-0.967
-0.237	-0.171	-0.0951
1.24	0.378	0.563
-0.186	-0.13	-0.188
-0.276	-0.191	-0.126
0.0368	0.0203	0.0299
-0.492	-0.18	-0.184
-0.0356	-0.0168	-0.0115
0.711	0.48	0.312
0.331	0.127	0.174
-1.12	-0.42	-0.591
-2.56	-0.83	-0.818
-0.658	-0.286	-0.164
0.891	0.35	0.278
-0.291	-0.182	-0.222
1.6	1.01	1.23
-1.21	-0.859	-0.831
-0.00831	-0.00615	-0.00542
-0.43	-0.172	-0.25
-0.8	-0.318	-0.343
0.401	0.254	0.225
0.318	0.147	0.172
-1.07	-0.538	-0.742
-0.0746	-0.0544	-0.0409
1.3	0.326	0.37
0.0425	0.0114	0.00614
-0.0178	-0.00456	-0.00668
-1.89	-0.616	-0.625
-1.05	-0.666	-0.869
1.16	0.613	0.724
-0.644	-0.352	-0.297
-1.48	-0.584	-0.526
0.113	0.0788	0.064
-0.888	-0.265	-0.278
-0.854	-0.509	-0.583
-0.921	-0.294	-0.348
1.66	0.554	0.603
0.139	0.0635	0.0656
0.843	0.605	0.895
0.163	0.086	0.0605
-0.486	-0.347	-0.319
-0.746	-0.428	-0.546
-0.793	-0.224	-0.318
0.299	0.0778	0.0809
-1.76	-0.666	-0.359
0.0866	0.0589	0.0726
0.13	0.0451	0.042
-1.33	-0.75	-0.963
-0.118	-0.0341	-0.0375
-1.16	-0.393	-0.512
0.172	0.0876	0.113
-0.952	-0.496	-0.403
0.145	0.0364	0.0343
-0.45	-0.169	-0.14
0.159	0.117	0.0749
-0.51	-0.37	-0.554
-0.402	-0.146	-0.108
0.526	0.218	0.219
-0.907	-0.279	-0.406
-2.32	-1.21	-1.64
-1.19	-0.804	-0.852
0.358	0.0916	0.0977
0.124	0.087	0.0518
-0.53	-0.176	-0.151
1.28	0.762	0.535
-0.442	-0.236	-0.247
-0.00543	-0.00289	-0.00363
-0.719	-0.253	-0.321
-0.525	-0.317	-0.305
-0.956	-0.542	-0.752
0.646	0.418	0.258
0.397	0.248	0.159

Insgesamt verteilen sich die Ergebnisse wie folgt:

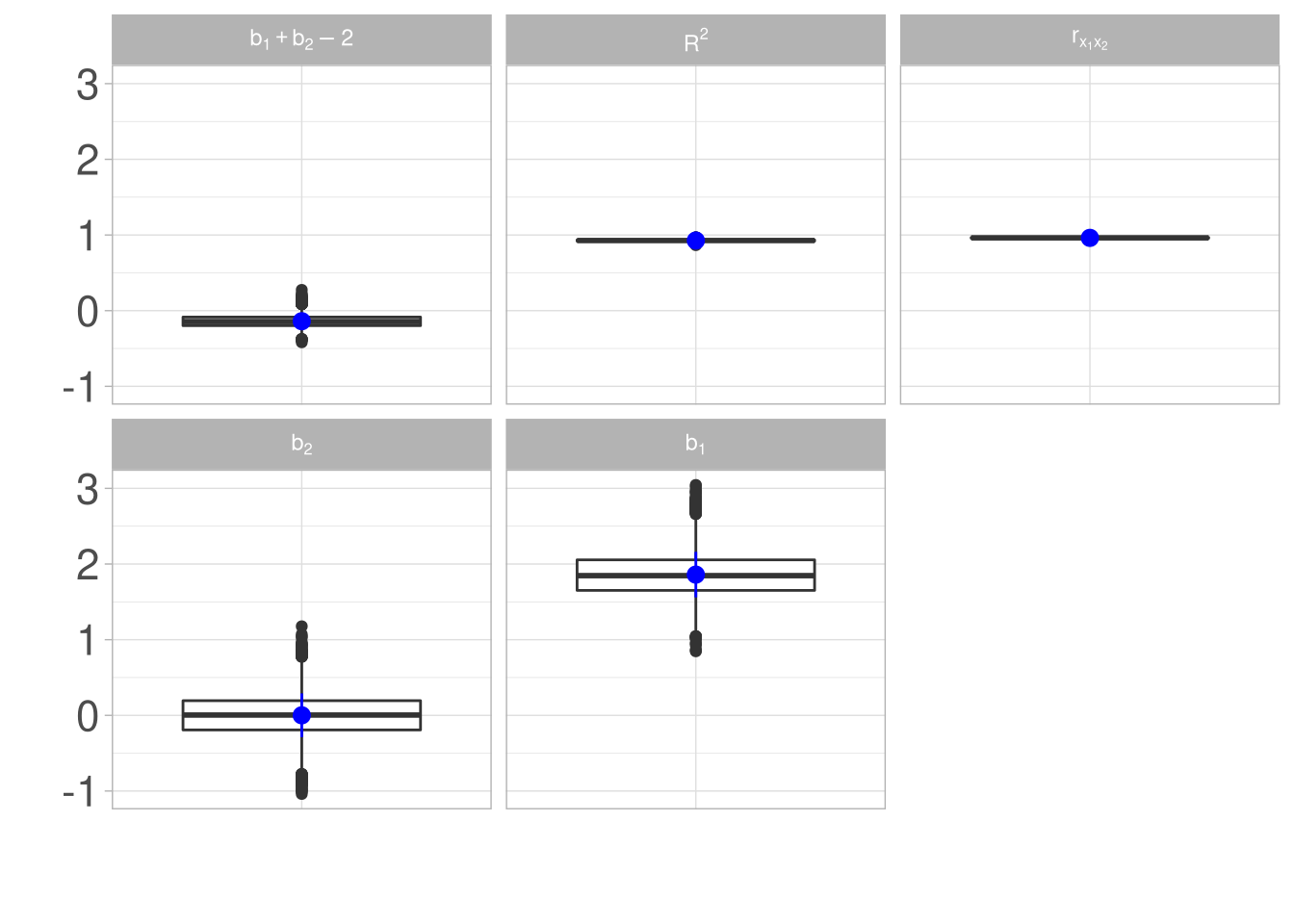
Gewisse Linearkombinationen der Koeffizienten sind deutlich stabiler als die Koeffizienten allein, wie man hier am Beispiel von \(b_1 + b_2 + 2\) gut sehen kann. Welche Linearkombination gerade besonders stabil sein könnte, kann man einfach an einer Punktwolke wie der folgenden ablesen:

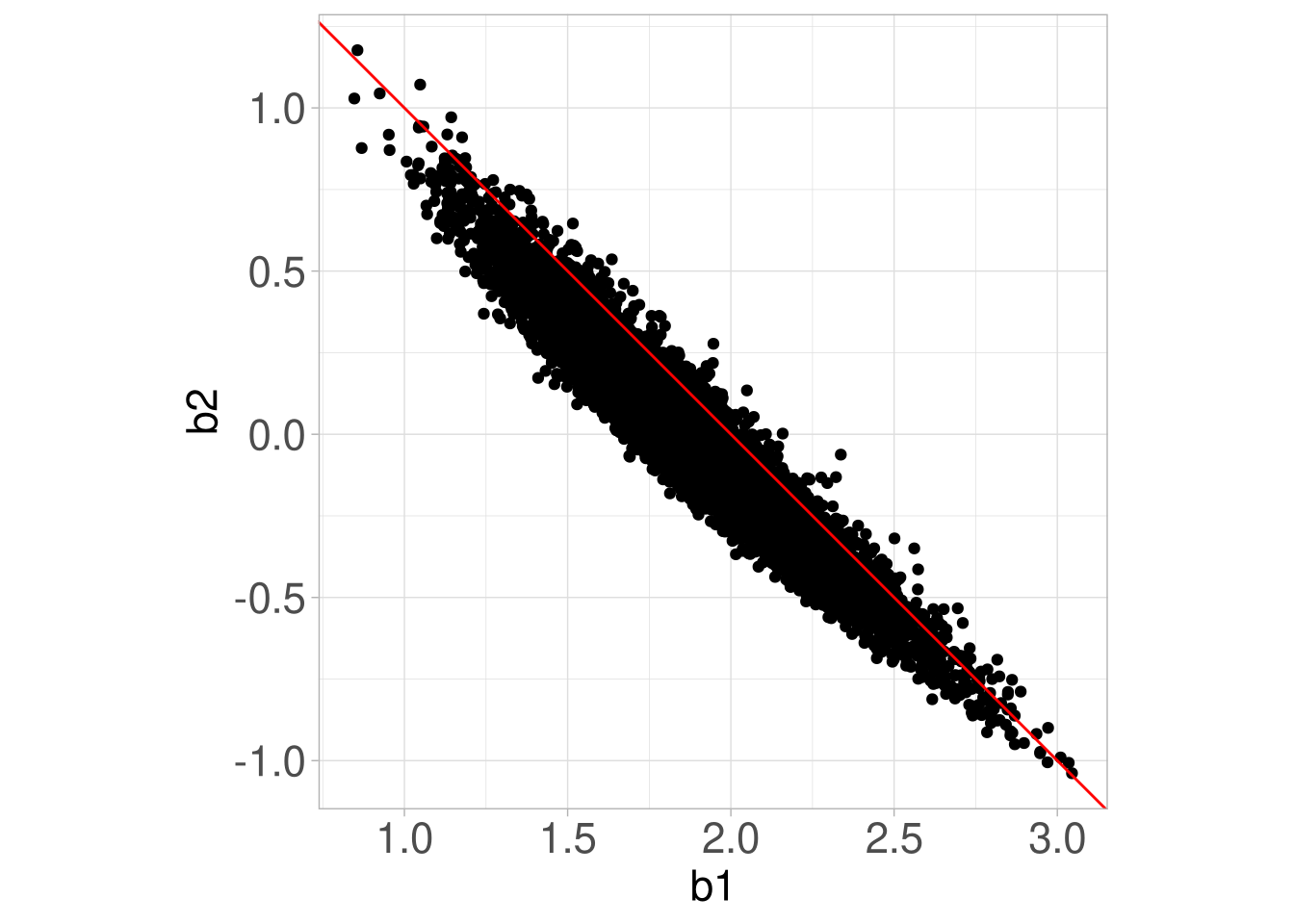
Paarweise lineare Zusammenhänge lassen sich anhand der Korrelationsmatrix der Prädiktoren prüfen.

df_wide %>% 
  select(hawie_iq,
         hawie_wahr_log) %>% 
  cor()

##                 hawie_iq hawie_wahr_log
## hawie_iq       1.0000000      0.7590665
## hawie_wahr_log 0.7590665      1.0000000

Faustregel: Korrelationen > 0.8 weisen auf starke Kollinearität hin.

Der Varianzinflationsfaktor \(\text{VIF}_j=\frac{1}{1-R_j^2}\) jedes Prädiktors \(j\) liefert eine weitere Möglichkeit zur Kollinearitätsdiagnostik. Er kann mit der Funktion vif() aus dem Paket car berechnet werden.

library(car)
vif(fit_post_il)

##       hawie_iq hawie_wahr_log 
##       2.359503       2.359503

Faustregel: VIF-Faktor > 4 \(\rightarrow\) starke Multikollinearität