Schleifen

Bei so gut wie allen Simulationsproblemen stehen wir vor der Situation, dass wir eine Operation, zum Beispiel das Generieren einer gewissen Zahl an Zufallswerten und die Berechnung der zugehörigen Teststatistik, mehrere hundert Mal ausführen wollen.

Wir könnten jetzt die Operation mehrere hundert mal in unser Skript schreiben, damit würden wir aber zum Einen Fehler einladen, zum Anderen viel zu viel Lebenszeit verschwenden.

Deswegen gibt es in so gut wie jeder Programmiersprache irgendeine Form von Ausdrücken, die eine iterative Wiederholung eines Ausdrucks ermöglichen.

Ein Beispiel für die Anweisung einer solchen iterativen Wiederholung sind Schleifen. In R gibt es davon drei Arten:

• repeat - die flexibelste Schleife, die so lange wiederholt bis sie mit break unterbrochen wird

• while - eine Schleife, die zu Beginn jeder Wiederholung einen logischen Test durchführt und bei Zutreffen die Operation wiederholt

• for - die unflexibelste der drei Möglichkeiten. for iteriert einen Wert durch einen Vektor oder eine Liste, bis alle Einträge einmal dran waren. Das heißt, dass wir eine feste Laufzeit und damit den einfachsten Umgang haben, weswegen wir auch for in diesem Kurs verwenden werden.

Die for-Syntax sieht dabei wie folgt aus:

for(value in vector){
  do something
}

Um jetzt Beispielsweise alle Werte von eins bis zehn durch zu laufen und jeden Wert auszugeben können wir den folgenden Ausdruck benutzen:

for(i in seq_len(10)){
  print(i)
}

## [1] 1
## [1] 2
## [1] 3
## [1] 4
## [1] 5
## [1] 6
## [1] 7
## [1] 8
## [1] 9
## [1] 10

Wie man an diesem Beispiel schon sehen kann, können wir in der Schleife auf den i-Wert zugreifen. Das können wir zum Beispiel benutzen, um die ersten zehn Zahlen der Fibonacci-Reihe zu berechnen, in der jeder Wert die Summe der zwei vorhergegangenen ist:

fib <- numeric(10)
for(i in seq_along(fib)){
  if(i<3){ # die ersten zwei Stellen müssen Einsen sein
    fib[i] <- 1
  }else{
    fib[i] <- fib[i-1] + fib[i-2] # nimm die letzten zwei Einträge und summier sie auf
  }
}
fib

##  [1]  1  1  2  3  5  8 13 21 34 55

In diesem Beispiel ist noch ein weiteres Programmier-Prinzip sichtbar, die Allokation des Ergebnis-Vektors vor der Berechnung der Werte. Damit ist einfach gemeint, dass wir den leeren fib-Vektor erstellt haben, bevor wir mit der Schleife angefangen haben.

Der Grund für dieses Vorgehen ist, dass jedes Anlegen eines Vektors einer bestimtmen Größe ein bisschen Rechenzeit kostet. Wenn wir von vornherein festlegen, wie lang der Vektor werden soll, müssen wir nur einen Vektor anlegen. Wenn wir stattdessen wie im folgenden Beispiel in jeder Iteration den Vektor vergrößern, erstellt R implizit in jeder Iteration einen neuen Vektor.

fib <- 1
for(i in seq_len(10)){
  if(i<3){ 
    fib[i] <- 1
  }else{
    fib[i] <- fib[i-1] + fib[i-2] 
  }
}
fib

##  [1]  1  1  2  3  5  8 13 21 34 55

Bei 10 Stellen ist der Unterschied noch nicht wirklich bemerkbar. Wenn wir jetzt aber das ganze in Funktionen verpacken und für längere Sequenzen laufen lassen und die Laufzeit stoppen sehen wir den Unterschied:

fib_alloc <- function(n){
  fib <- numeric(n)
  for(i in seq_along(fib)){
    if(i<3){ 
      fib[i] <- 1
    }else{
      fib[i] <- fib[i-1] + fib[i-2] 
    }
  }
  return(fib)
}


fib_no_alloc <- function(n){
  fib <- 1
  for(i in seq_len(n)){
    if(i<3){ 
      fib[i] <- 1
    }else{
      fib[i] <- fib[i-1] + fib[i-2] 
    }
  }
  return(fib)
}
start <- Sys.time()
a <- fib_alloc(100000)
runtime_alloc <- Sys.time() - start
start <- Sys.time()
b <- fib_no_alloc(100000)
runtime_no_alloc <- Sys.time() - start

runtime_alloc

## Time difference of 0.04131174 secs

runtime_no_alloc

## Time difference of 0.06902266 secs

Mehr als die Hälfte der Zeit geht für das Erstellen des neuen Vektors drauf!

Aufgabe

In QM-2 habt Ihr im Rahmen des zentralen Grenzwertsatzes gelernt, dass die Verteilungsfunktion der z-Transformation der n-ten Summe einer Reihe von unabhängigen Zufallsvariablen für wachsendes n schwach gegen die Standardnormalverteilung konvergiert.

Schreibe eine Funktion, die für eine gegebene Anzahl an Summen und eine gegebene Verteilungsklasse (und den entsprechenden Parametern inklusive der Stichprobengröße) einen Vektor mit den entsprechenden Summen zurückgibt. Nutze dafür deine Funktion aus der letzten Aufgabe.

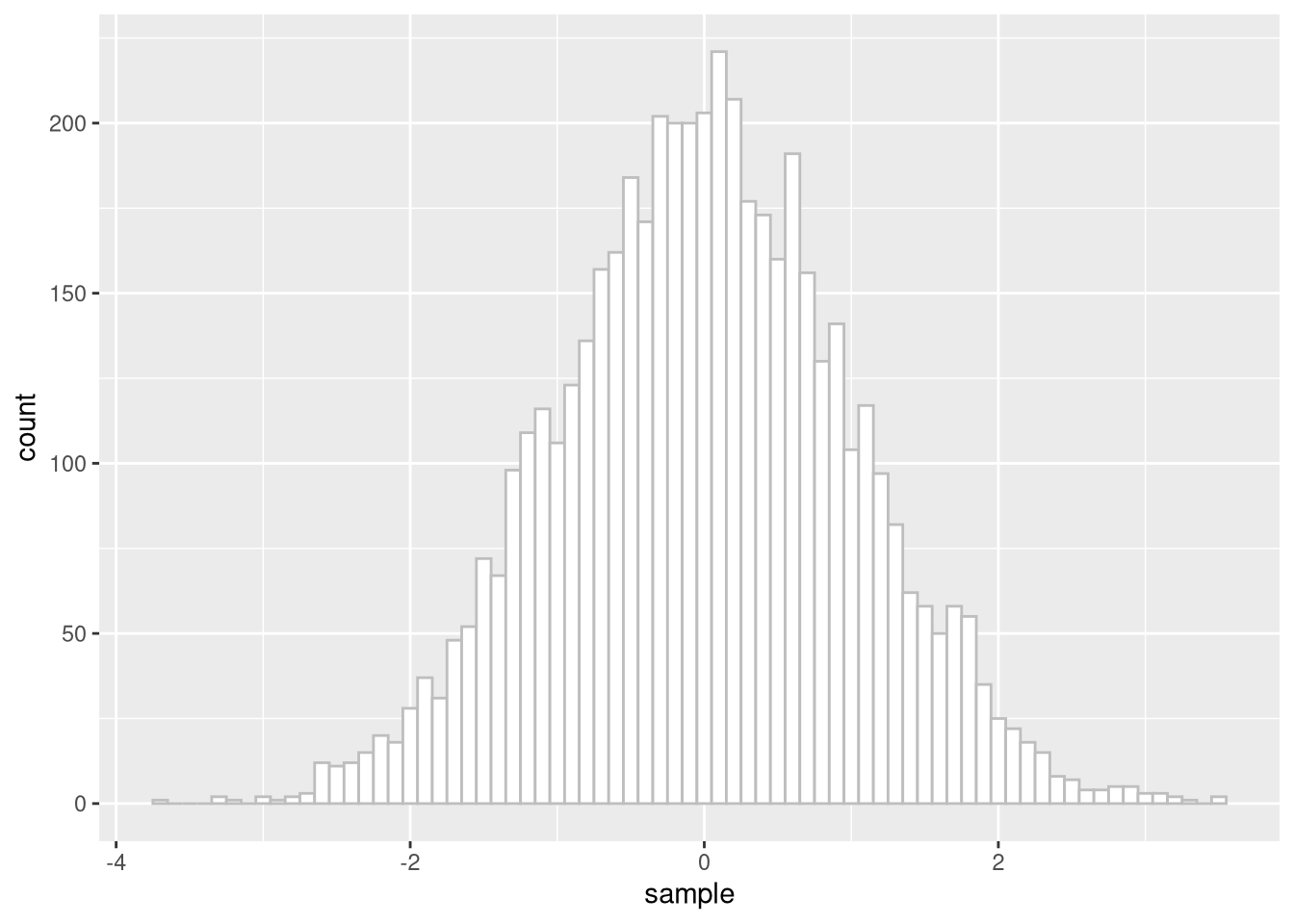
Nutze diese Funktion dann um ein Histogramm mit 5000 dieser z-transformierten Summen zu erstellen.

Antwort

gen_central_lim_vec <- function(N, 
                                distribution,
                                n,
                                df = 1,
                                lambda = 25,
                                rate = 5) {
  
  ret_vec <- numeric(N)
  for(i in seq_len(N)){
    ret_vec[i] <- sum(gen_distributed_values(distribution,
                                      n,
                                      df,
                                      lambda,
                                      rate))
  }
  return(ret_vec)
}

tibble(sample = scale(gen_central_lim_vec(5000, 'exp', 1000,rate = 5))) %>% 
  ggplot(aes(x = sample)) +
  geom_histogram(binwidth = .1,
                 color = 'grey',
                 fill = 'white')